Numeerinen matematiikka
Numeerinen matematiikka on se osa-alue, jossa ei pyöritellä kaavoja ja symboleja, vaan lasketaan raakasti luvuilla. Eli juuri se alue, jossa tietokone on hakannut ihmisen mennen tullen keksimisestään lähtien. Koska C/C++:n ominaisuudet numeerisen matematiikan käsittelyyn eivät ole aivan huippua, toisin kuin esimerkiksi sellaisessa kielessä kuin Fortran, ajattelin teidän opetuslapsien tarvitsevan jonkinlaista avustusta tässä asiassa - vaikka tarkasti ottaen eihän tämä enää C++-kieleen liitykään.
Näitä numeerisen matematiikan labyrinttejä harhaillessa lyhtynäni on heilunut alan suuri opus; Numerical Recipes in C, Second Edition [Press, Teukolsky, Vetterling, Flannery]. Se on suositeltava hankinta jokaiselle numeroita pyörittelevälle C++-ohjelmoijalle, tosin vaikean sisältönsä vuoksi ei mikään ensimmäinen hankinta aloittelijalle.
Sattuu ja tapahtuu - satunnaislukugeneraattorit
Kuten lupasin, nyt pureudumme syvemmälle satunnaisuuden olemukseen. Käytännönläheisempi tarinointi löytyy Standardikirjastot-osiosta. Aluksi meidän pitää pohtia satunnaisuuden todellista luonnetta - emmehän voi tyytä mihinkään sattumanvaraisiin satunnaisuuden määritelmiin. Tietokoneen toiminta ei ole satunnaista - se kaikki irrationaalinen Windowsin kaatuilu ei oikeasti ole satunnaista, vaan pelkästään vaikuttaa siltä. Tietokoneeseen voi kytkeä kuitenkin kaikenlaisia analogisia vatkaimia, joiden avulla yhteys todelliseen ja (mahdollisesti) satunnaiseen maailmaan on mahdollinen.
Kovin paljon tätä mahdollisuutta kytkeä ulkoisia satunnaislähteitä ei ole hyödynnetty - ymmärrettävästi, onhan se sen verran työlästä. Joidenkin salausprojektien yhteydessä, kun on tarvittu aivan äärimmäistä satunnaisuutta, on käytetty hyvin omaperäistä ja jopa hippiaikoja sivuavaa järjestelmää. Kaiken ytimenä on toiminut laavalamppu, tuo yltäkylläisesti hinnoiteltu sisustuselementti. Lamppu koostuu valaistusta säiliöstä, jossa kiinteämpää ainetta olevat möykyt vellovat ja muuttavat muotoaan. Liikkeet ovat hyvin satunnaisia. Sitten tarvitsemme vain digitaalikameran, joka kuvaa laavan liikkeitä. Nyt meillä on digitaalista tietoa analogisesta ja satunnaisesta tapahtumasta. Sitä käsittelemällä voimme luoda todella satunnaisen satunnaislukugeneraattorin. Tiettävästi lamppuja oli vielä useita ja niiden tuottamaa satunnaisdataa yhdistettiin.
X=(aI + c) mod m
a, c ja m ovat huolella valittuja vakioita. Siis edellinen luku kerrotaan a:lla, lisätään siihen c ja otetaan jakojäännös osamäärästä luvun m kanssa. Kaava on hyvin yksinkertainen ja tietokone suorittaa satunnaislukujen luonnin nopeasti ja tuottaa säädyllisen satunnaisia lukuja, mutta systeemi on silti ihan syvältä vaativammissa tehtävissä. Jos siis tarvitsemme todellista satunnaisuutta, kuten asianlaita on mm. simuloidussa jäähdytyksessä (simulated annealing), pitää rand() jättää väliin. Sen pahin teoreettinen puute on satunnaislukujen jaksollisuus. Käytännössä suurin vika on pieni m:n arvo.
Millaista sitten on hyvä satunnaisuus? Satunnaislukugeneraattorien tuottamien lukujen tulisi pidemmän päälle noudattaa tasajakaumaa (uniform deviation). Kun siis arvotaan monta lukua, pitäisi jokaista lukua tulla lähes yhtä paljon. Myös muunlaisia jakaumia voi käyttää, normaalijakauma tärkeimpänä. Normaalijakauma noudattaa Gaussin käyrää, siis suurin osa arvoista on keskittyneenä keskivaiheille ja aivan äärilaidoissa arvoja on vähän. Normaalijakaumaa noudattelee moni luontoon ja todellisuuteen liittyvä asia, kuten ihmisten pituus. Se onkin sopiva väline simuloidessa vaikka sääolosuhteita lentopelissä - yleensä on normaalisää, mutta myrskytkään eivät ole täysi mahdottomuus. Kaiken pohjana yleensä kuitenkin on tasajakauma, josta erilaisilla operaatioilla saadan erikoistuneempia satunnaislukujen jakaumia.
Jaksollisuudestaan johtuen rand() voi sopivissa olosuhteissa tuottaa hyvin heikkoa jakaumaa - tietyt arvot ovat toisia yleisempiä. Tietyt olosuhteet ovat voimassa esimerkiksi silloin, kun satunnaisluvut jaetaan järjestelmällisesti joka kierroksella: huonolla tuurilla tietty jaksollisuus luvuissa voi moninkertaistua - näin on esimerkiksi koulutettaessa neuroverkkoja simulated annealing algoritmilla. Suurempi ongelma varsinkin arkiohjelmoijalle on kuitenkin m, kääntäjän vakio RAND_MAX. Generaattori palauttaa luvun väliltä 0 - RAND_MAX. 16-bittisten aikojen perintönä RAND_MAX hyvin yleisesti on 2^15=32767. Se ei itseasiassa ole paljon. Mikäli mielii saada suurempia satunnaislukuja, joutuu monta generoitua satunnaislukua yhdistämään ja siinä touhussa saa olla tarkka, ettei hävitä sitä satunnaisuutta mitä generaattorista saa.
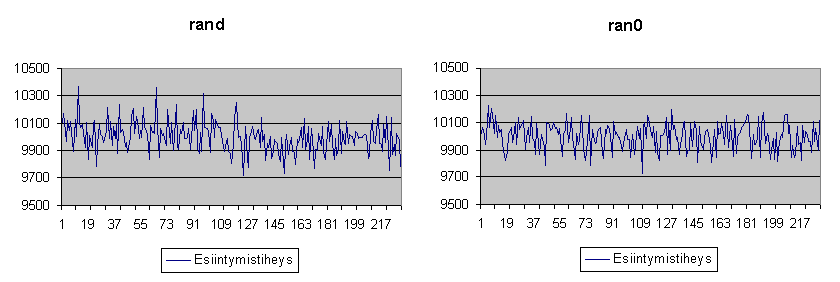
Otin sitten ja tein pienen ohjelman satunnaislukugeneraattorien testaamiseen. Se tuottaa lukuja kääntäjän mukana tulleella generaattorilla ja toisella, Minimal Standard -algoritmiin perustuvalla generaattorilla. Tulokset kirjataan tiedostoon, josta sitten syötin ne Excelille ja piirtelin jakaumat. Kyseessä tulisi olla tasajakauma, siis viivan pitäisi olla mahdollisimman suora ja tasainen.

Kuten huomaat, ran0 (Minimal Standard) tuottaa ihan hivenen tasaisempaa jälkeä. Kun lukuja arvottiin 2 300 000 kappaletta väliltä 0 - 230, jokaisen luvun tulisi siis toistua keskimäärin 10 000 kertaa, olivat poikkeamien keskiarvot: rand: 82,7 ja ran0: 78,4. Siis ran0 oli hivenen parempi. Tosin voi spekuloida, olisiko ero tullut selvemmäksi mikäli suorituskertojen määrää olisi vielä lisätty. Mikäli vaikka haluat kokeilla sitä tai muuten vaan tutustua testikalustoon, on käyttämäni ohjelman listaus saatavilla - samoin kuin aiheesta tuherrettu Excel-taulukko. Ohjelma kertoo myös RAND_MAX:in arvon. [rands.cpp - rands.xls]
Pitää kuitenkin muistaa, että on epätodennäköistä, että "täydellinen" satunnaislukugeneraattori tuottaa täysin tasaista jälkeä rajallisella otosten määrällä. Siksi jakaumien tarkastelu ei ole paras tai edes mitenkään erityisen hyvä tapa tarkastella generaattorien paremmuutta - toki sillä löytää pahat mokat mikäli esimerkiksi joutuu itse kehittelemään oman generaattorinsa johonkin erityistarkoitukseen. George Marsaglia niminen satunnaisuusmies on kehittänyt joukon testejä, joilla erotetaan jyvät apinoista (puhumme siis yhä erilaisista satunnaislukugeneraattoista). Tasajakauman lisäksi niihin kuuluu parien, kolmikoiden jne... esiintymisten tasaisuus, pitkien jonojen esiintymättömyys rajatuissa otoksissa ja monia muita menetelmiä. Lisää aiheesta voi lukea vaikka kirjasta Satunnaisuuden viidakot [Terra Cognita 1998: Peterson, suom. Pietiläinen].